わっけわかんねえほど沢山の制約ドパァな問題を解く一般的なテクとして、
なんかいい感じのグラフを作ったらなんかそれの最小カットが答え
というのがあります
最小カットで解ける問題はどんなのなのか考えてみました
頂点がたくさんあって、それを赤と青に塗り分けるという問題を考えます。燃やすと埋めるでも大丈夫です
最小カットで解ける問題というのは、実は
- 頂点がたくさんある。それを赤と青に塗り分ける。全部の頂点を必ず赤か青に塗らなくてはいけない
- 必ず赤色に塗らなくてはいけない頂点(Sとする)と青色に塗らなくてはいけない頂点(Tとする)が存在する
- 「Xが赤で、Yが青の時にZ円の罰金がかかる」という制約が沢山ある
- 罰金の最小値は?
という問題だけです。
これの解法は、
- 「Xが赤で、Yが青の時にZ円の罰金がかかる」ならX->Yに容量Zの辺を貼る
- SからTに最大流
- 流せた量が答え
処理できる条件は「Xが赤で、Yが青の時にZ円の罰金」だけでスタートしていきます
例題1
- 頂点A, B, Cがある
- Aは赤に塗るのに50円, 青に塗るのに80円かかる
- Bは赤に塗るのに30円, 青に塗るのに40円かかる
- Cは赤に塗るのに100円, 青に塗るのに70円かかる
- 全部赤か青のどちらかに塗る。コストを最小化せよ
答えは 50 + 30 + 70 = 150
これは貪欲法で解けるのですが、まぁ最小カットで解いてみましょう
「Aは赤に塗るのに50円, 青に塗るのに80円」,つまり「Aが赤なら50円罰金, Aが青なら80円罰金」という制約を
「Xが赤で、Yが青の時にZ円の罰金」という制約に直せば解けます
ここで、Sは必ず赤色、Tは必ず青色であることを使うと
「Aが赤なら50円罰金, Aが青なら80円罰金」というのは
「Aが赤でTが青なら50円罰金」かつ「Sが赤でAが青なら80円罰金」となります
これで最小カットになりました、次のようなグラフになります
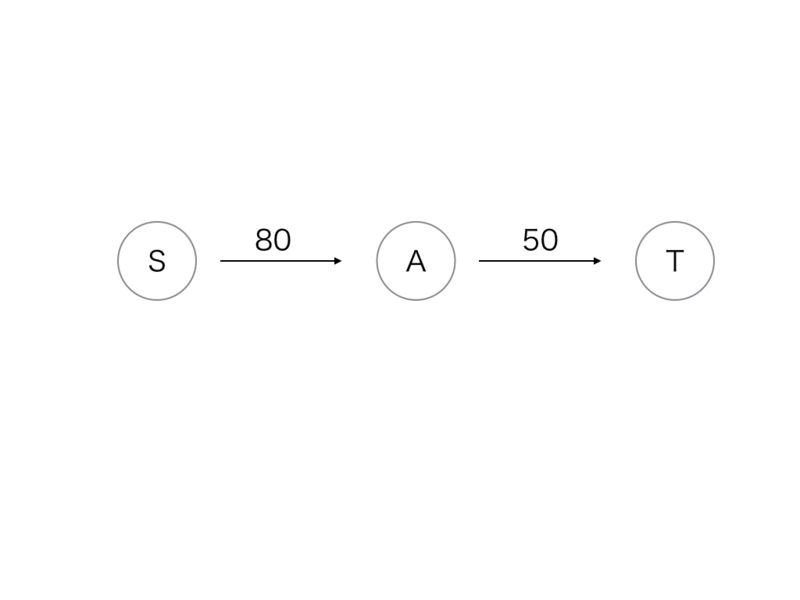
これをBとCにもやると、次のようなグラフになります
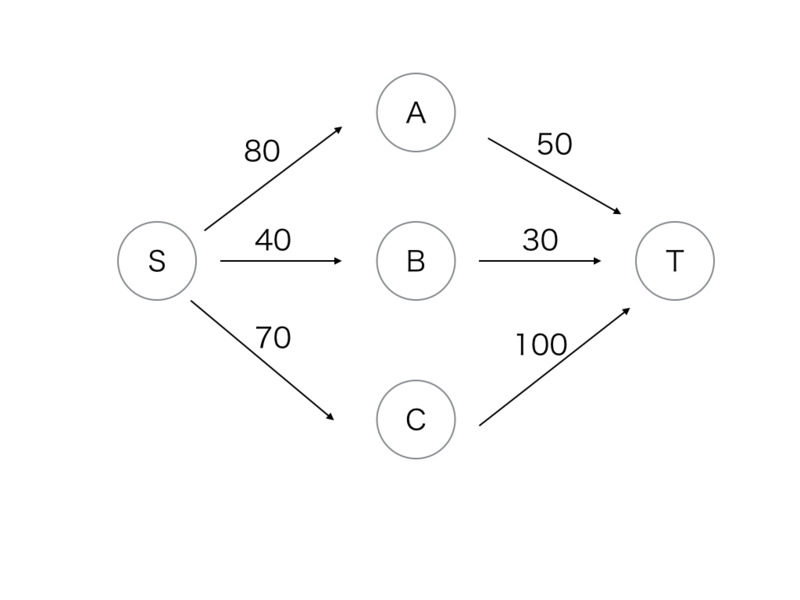
これの最大流はちゃんと150になってます(あたりまえ)
これで、
「Xが赤で、Yが青の時にZ円の罰金」
「Xが赤色ならZ円の罰金」
「Xが青色ならZ円の罰金」
を処理できるようになりました
例題2
- 頂点A, B, Cがある
- Aは赤に塗るのに50円, 青に塗るのに80円かかる
- Bは赤に塗るのに30円, 青に塗るのに40円かかる
- Cは赤に塗るのに100円, 青に塗るのに70円かかる
- Aが赤色でBが青色の時は70円の罰金
- Bが赤色でAが青色の時は40円の罰金
- Cが赤色でBが青色の時は30円の罰金
- 全部赤か青のどちらかに塗る。コストを最小化せよ
例題1に比べて制約が3つ増えました。これだと問題感が出てきましたね
でも最小カットで解くとわかっていると簡単です。
以下のグラフのようになります
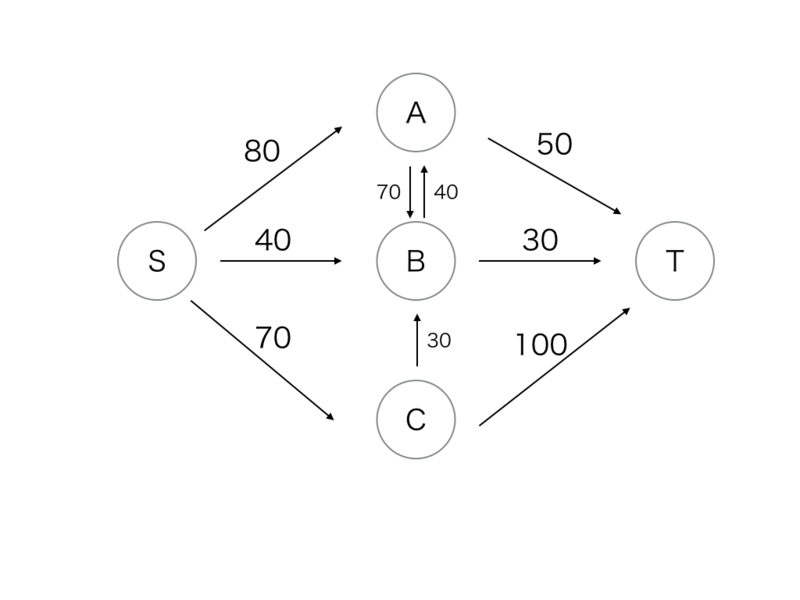
例題3
- 頂点A, B, Cがある
- Aは赤に塗るのに50円, 青に塗るのに80円かかる
- Bは赤に塗るのに30円, 青に塗るのに40円かかる
- Cは赤に塗るのに100円, 青に塗るのに70円かかる
- Aが赤色でBが青色の時は70円の罰金
- Bが赤色でAが青色の時は40円の罰金
- Cが赤色でBが青色の時は30円の罰金
- Aが赤色でCが赤色の時は120円の報酬
- 全部赤か青のどちらかに塗る。コストを最小化せよ
「Aが赤色でCが赤色の時は120円の報酬」という制約が加わりました
なので、「Aが赤色でCが赤色の時は120円の報酬」というのをどうにかしなければいけません
なんで罰金じゃなくて報酬かというとそっちの方が簡単だからです
「Aが赤色でCが赤色の時は120円の報酬」は新たな頂点Dを生み出して、
「問答無用で120円貰える」
「Dが青色だと120円罰金」
「Dが赤色の時、必ずAとCは赤色」
と同じになります。技巧的ですね
Dが赤色の時は120円貰えて、AとCは必ず赤色になります
Dが青色の時は120円罰金ですが、120円貰えてチャラ、そしてAとCの色に制約はありません
つまり
D赤->+120 AとCは必ず赤色
D青-> 0 AとCは何色でもいい
よって「Aが赤色でCが赤色の時は120円の報酬をもらっても良い」という条件と等しくなります。
コスト最小化なのでこれは当然「Aが赤色でCが赤色の時は120円の報酬」という条件と等しいですね。
では、「Dが赤色の時、必ずAとCは赤色」をどうするか考えましょう
これは簡単で、
「Dが赤色でAが青色だと五億円の罰金」
「Dが赤色でCが青色だと五億円の罰金」
と等しいです。
以上まとめて
「Aが赤色でCが赤色の時は120円の報酬」
=
「問答無用で120円貰える」
「Dが青色だと120円罰金」
「Dが赤色でAが青色だと五億円の罰金」
「Dが赤色でCが青色だと五億円の罰金」
となります。
また、
「Aが青色でCが青色の時は120円の報酬」
=
「問答無用で120円貰える」
「Eが赤色だと120円罰金」
「Aが赤色でEが青色だと五億円の罰金」
「Cが赤色でEが青色だと五億円の罰金」
となります。
これで、
「Xが赤で、Yが青の時にZ円の罰金」
「Xが赤色ならZ円の罰金」
「Xが青色ならZ円の罰金」
「Xが赤で、Yが赤の時にZ円の報酬」
「Xが青で、Yが青の時にZ円の報酬」
を処理できるようになりました
多分
「Xが赤で、Yが青ならZ円の報酬」
「Xが赤で、Yが赤ならZ円の罰金」
は最大カットになって解けないと思います。
問題を解いてみる
D: 浮気予防 - AtCoder Beginner Contest #010 | AtCoder
を解いてみましょう。
この問題は
chokudaiと男沢山と女沢山がSNSで繋がってる
chokudaiと女の関係(これはchokudai-男-男-女みたいなのも含む)を全部消したい
1円で女を抹消できる
1円で人間関係を1個破壊できる
みたいな感じです。
chokudaiは必ず赤色、つまりSとして
男と女を赤色(chokudaiと関係がある)と青色(chokudaiと関係がない)に塗ることを考えます
すると
「女は赤色だと(最終的に個別に抹消しなければいけないため)1円かかる」
「元から関係がある頂点について、片方が赤色で片方が青色だと(その間の関係を抹消したことになるため)1円かかる」
となり解けます
まとめ
「Xが赤でYが青だとZ円罰金」
X->Yに容量Zの辺を貼る
「Xが赤 or 青だとZ円罰金」
赤だと罰金:X->Tに容量Zの辺
赤だと罰金:S->Xに容量Zの辺
おわりに
http://community.topcoder.com/stat?c=problem_statement&pm=13680
これはSRM653のDiv1Med(450)ですが、最小カットとわかっているとthe やるだけです
診断人さんのスライド
最小カットを使って「燃やす埋める問題」を解く
をめっちゃ参考にしました