概要
3*Nの行列が与えられる。
K回、以下の動作ができる。
- 異なるi, j, kを選ぶ。(1, i)と(2, j)と(3, k)の値を1ずつ減らす。
どういう行列なら、すべての値を0以下にできるか?
というのが本質部分です。
これについて考えていたら、面白い結論が出たのでメモします。
解法
実は、すべての列とすべての行について値の総和がK以下であることが必要十分です。
一般化
N*Nの値が非負整数の行列が与えられる。
K回、以下の動作ができる
- 順列a1, a2, ..., aNを選ぶ。(ai, i)の値を1減らす。
どのような行列ならばすべての値を0にできるか?
思考
実はこの問題も同様に、すべての列と行について値の和はKであることが必要十分になるはずです。
数学的帰納法で考えると、以下のような問題になります。
N*Nの行列が与えられ、すべての列と行について和の値はKである。
以下の条件を選ぶようにマス目をN個選べるか?
- どの列も1個選ばれてる
- どの行も1個選ばれてる
- どのマスの値も1以上である
こういう選び方をすれば、K -> K-1という遷移ができるのでOKです。
ここで、ネットワークフローを考えます。
左に頂点がN個、右に頂点がN個あります。s -> 左の頂点の容量と、右の頂点 -> tの容量は全て1、さらに、左の頂点から出て行く辺の容量と右の辺に流れ込む辺の容量の和は全てK。このようなグラフで必ず最大マッチングはNとなることがわかればOKです。
ですが、これはホールの結婚定理を使うときれいに示せます。左側の頂点を幾つか選んだ時に、対応する右側の頂点の集合の数は、辺の容量の和の制約から必ず左側の選んだ数より大きくなるからです。
元の問題
これが言えると元の問題が解けるのか?というと非自明です。(これだけでもD1easyくらいはありそう)
以下白字(にしたかったんですが、画像はどうしようもない)
3*Nの行列について、(列と行の値の和がK以下 => K回の取り除く動作で全て0以下になる)
が言えれば良い(逆は自明)。
3*Nの行列を、(3+N) * (3+N)の行列へ拡張することを考える。
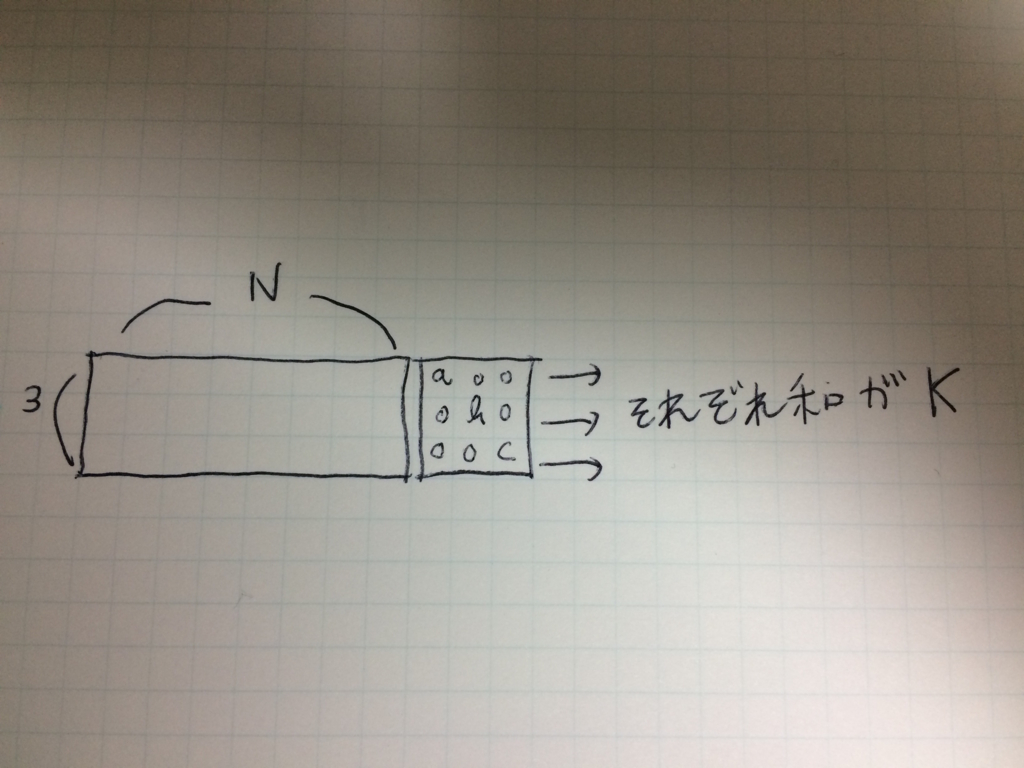
まず、3N -> 3(N+3)への拡張だが、これは下図のようにする。
いい感じにa, b, cを設定することで、行ごとの和が全てKになるようにできる。
このあと、下にN*(3+N)をくっつけるが、これもいい感じに加えると、全ての列の和がKになるようにできる。
これは一般化した問題なので、K回の取り除く動作で全部の値が0に出来る。その操作を3*Nの行列について取り出せば、いい感じ。