問題概要
問題
長さNのカッコ列 $a_1,a_2,\cdots,a_n$ が与えられる。これは正しく閉じているとは限らない。各文字は32bit非負整数の重み $b_1,b_2,\cdots,b_n$ を持っている。
カッコ列Sに対して、 $f(S)$ を次のように定義する
- $S$ が
()を部分文字列として持っているかぎりそれを削除し続ける、その時の最終的な文字列。
$f(S)$はどのindexの文字を残すかまで含めて一意に定まることに注意。
次の $Q$ 個のクエリを処理。
1 x y: $b_x$を $y$ に変更する(問題文には $a_x \to 1 - a_x$ もすると書かれているが、これは嘘)2 l r: $f(S[l..r])$ の重みを $c_1, c_2, \cdots, c_k$ としたときの、$\max (c_1, c_2, \cdots, c_k), \mathrm{nand}(...\mathrm{nand}(\mathrm{nand}(2^{32}-1, c_1), c_2), ..., c_k)$を求める。この2つをxorしたものを出力する。3 l r: $l..r$文字目と$r+1..n$文字目が入れ替わるようにswapする
制約
- $N \leq 2 \times 10^{6}$
- $Q \leq 2 \times 10^{5}$
解法
クエリ2で求めるmax / nandは共にモノイドの演算として考えることができる。
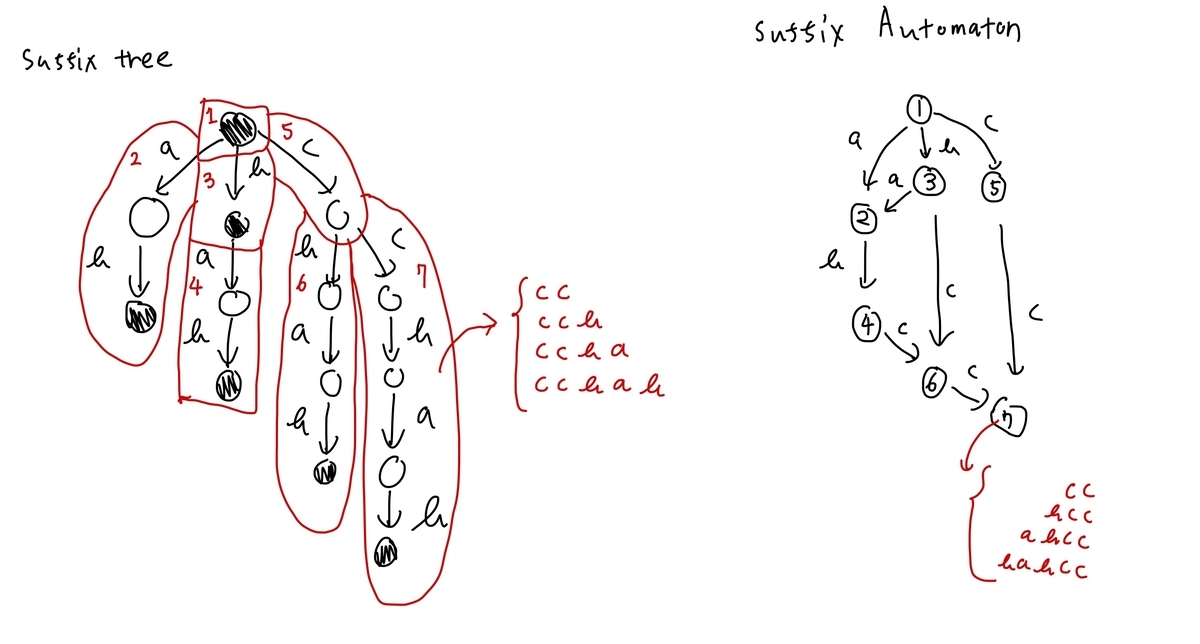
カッコ列から () を取り除き続けたときの最終的な文字列の長さが平衡二分木に乗るのはそこそこ有名。最終的な文字列は ))..)(..((という形になるので、 )と ( の個数を x, y とすると、 op((lx, ly), (rx, ry)) = (lx + rx - min(ly, rx), ly + ry - min(ly, ry) のような演算ができる。
今回の問題で同様のことをすると、ノードごとに
))..)の長さ ln((..(の長さ rn))..)の重みの総和 lval((..(の重みの総和 rval
を持たせたくなるけど、これだとうまくノードがマージできない。
ここで、次の3つのパターンに限ればmerge可能なことに注目する。
l->rn = 0r->ln = 0l->rn = r->ln
「すべての葉以外のノードがこの3つの条件のいずれかを満たす」ような、葉に値を持たせる平衡二分木を管理する。
この追加条件を保つようにsplay treeを改造する。
方針としては、次のクエリを実装する。
lsplit(node, k): ノードを2つに分割する。左のノードに対応する文字列 $S$ について、$f(S)$ は ))..) ($k$ 文字)。rsplit(node, k): ノードを2つに分割する。右のノードに対応する文字列 $S$ について、$f(S)$ は ((..(($k$ 文字)。
これらの関数が実装できると、通常の平衡二分木のようにmergeが実装できる。mergeの引数が上記の3条件を満たさない場合でも、lsplitかrsplitを呼ぶことでmerge可能な形に変形できる。
lsplitやrsplitは、このmerge関数が実装できれば実装できる。つまり相互再帰みたいな感じになる。
計算量
何もかもが謎
- 手元で適当に試すと $O(\log N) / \mathrm{query}$ っぽい挙動をするが、はたして…
- 実はもう少し違う方針で $O(\log ^2 N) / \mathrm{query}$ は達成できるが、これはTLEした
- writer解も謎のsplay treeっぽいことをしていた、editorialがないのでこれも計算量は謎
コード
#include <cstdio>
#include <cassert>
#include <memory>
#include <algorithm>
#include <vector>
using namespace std;
using uint = unsigned int;
struct Monoid {
uint mx, zero, one;
Monoid() {
mx = 0;
zero = 0;
one = -1;
}
Monoid(uint x) {
mx = x;
zero = -1;
one = ~x;
}
uint eval() { return mx ^ one; }
};
Monoid operator+(const Monoid& l, const Monoid& r) {
Monoid m;
m.mx = max(l.mx, r.mx);
m.zero = (l.zero & r.one) | (~l.zero & r.zero);
m.one = (l.one & r.one) | (~l.one & r.zero);
return m;
}
struct Node;
using NP = unique_ptr<Node>;
struct Node {
NP l = nullptr, r = nullptr;
int sz = -1;
int ln, rn;
Monoid lval, rval;
Node() {}
Node(bool type, uint x) : sz(1) {
if (!type) {
ln = 1;
rn = 0;
lval = Monoid(x);
rval = Monoid();
} else {
ln = 0;
rn = 1;
lval = Monoid();
rval = Monoid(x);
}
}
Node(NP _l, NP _r) : l(move(_l)), r(move(_r)), sz(l->sz + r->sz) {
assert(l && r);
if (l->rn == r->ln) {
ln = l->ln;
rn = r->rn;
lval = l->lval;
rval = r->rval;
} else if (l->rn == 0) {
ln = l->ln + r->ln;
rn = r->rn;
lval = l->lval + r->lval;
rval = r->rval;
} else if (r->ln == 0) {
ln = l->ln;
rn = l->rn + r->rn;
lval = l->lval;
rval = l->rval + r->rval;
} else {
assert(false);
}
}
};
pair<NP, NP> lsplit(NP x, int k);
pair<NP, NP> rsplit(NP x, int k);
NP merge(NP l, NP r) {
if (!l) return r;
if (!r) return l;
if (l->rn == 0 || r->ln == 0 || l->rn == r->ln) {
return NP(new Node(move(l), move(r)));
}
if (l->rn < r->ln) {
auto u = lsplit(move(r), l->rn);
return NP(
new Node(NP(new Node(move(l), move(u.first))), move(u.second)));
} else {
auto u = rsplit(move(l), r->ln);
return NP(
new Node(move(u.first), NP(new Node(move(u.second), move(r)))));
}
}
template<class F>
pair<NP, NP> split2(NP x, F f) {
int type = f(x);
if (type == 0) {
return {move(x->l), move(x->r)};
}
if (type == -1) {
int type2 = f(x->l);
if (type2 == 0) {
return {move(x->l->l), merge(move(x->l->r), move(x->r))};
}
if (type2 == -1) {
auto u = split2(move(x->l->l), f);
return {move(u.first),
merge(move(u.second), merge(move(x->l->r), move(x->r)))};
} else {
auto u = split2(move(x->l->r), f);
return {merge(move(x->l->l), move(u.first)),
merge(move(u.second), move(x->r))};
}
} else {
int type2 = f(x->r);
if (type2 == 0) {
return {merge(move(x->l), move(x->r->l)), move(x->r->r)};
}
if (type2 == 1) {
auto u = split2(move(x->r->r), f);
return {merge(merge(move(x->l), move(x->r->l)), move(u.first)),
move(u.second)};
} else {
auto u = split2(move(x->r->l), f);
return {merge(move(x->l), move(u.first)),
merge(move(u.second), move(x->r->r))};
}
}
}
pair<NP, NP> lsplit(NP x, int k) {
assert(0 <= k && k <= x->ln);
if (k == 0) {
return {nullptr, move(x)};
} else if (k == x->ln) {
return {move(x), nullptr};
}
return split2(move(x), [&](const NP& n) {
assert(0 < k && k < n->ln);
int lsz = n->l->ln;
if (lsz == k) return 0;
if (k < lsz) return -1;
k -= lsz;
return 1;
});
}
pair<NP, NP> rsplit(NP x, int k) {
assert(0 <= k && k <= x->rn);
if (k == 0) {
return {move(x), nullptr};
} else if (k == x->rn) {
return {nullptr, move(x)};
}
return split2(move(x), [&](const NP& n) {
assert(0 < k && k < n->rn);
int rsz = n->r->rn;
if (rsz == k) return 0;
if (k < rsz) return 1;
k -= rsz;
return -1;
});
}
pair<NP, NP> split(NP x, int k) {
assert(0 <= k && k <= x->sz);
if (k == 0) {
return {nullptr, move(x)};
} else if (k == x->sz) {
return {move(x), nullptr};
}
return split2(move(x), [&](const NP& n) {
assert(0 < k && k < n->sz);
int lsz = n->l->sz;
if (lsz == k) return 0;
if (k < lsz) return -1;
k -= lsz;
return 1;
});
}
int main() {
int n, q;
scanf("%d %d", &n, &q);
vector<int> a(n);
vector<uint> b(n);
for (int i = 0; i < n; i++) {
scanf("%d %d", &(a[i]), &(b[i]));
}
auto build = [&](auto self, int l, int r) -> NP {
if (l + 1 == r) {
return NP(new Node(a[l] == 1, b[l]));
}
int mid = (l + r) / 2;
return merge(self(self, l, mid), self(self, mid, r));
};
NP tr = build(build, 0, n);
for (int ph = 0; ph < q; ph++) {
int ty, l, r;
scanf("%d %d %d", &ty, &l, &r);
l--;
if (ty == 1) {
auto t0 = split(move(tr), l + 1);
auto t1 = split(move(t0.first), l);
assert(t1.second->sz == 1);
*t1.second = Node(t1.second->rn == 1, r);
tr = merge(merge(move(t1.first), move(t1.second)), move(t0.second));
} else if (ty == 2) {
auto t0 = split(move(tr), r);
auto t1 = split(move(t0.first), l);
auto val = t1.second->lval + t1.second->rval;
printf("%u\n", val.eval());
tr = merge(merge(move(t1.first), move(t1.second)), move(t0.second));
} else {
auto t0 = split(move(tr), r);
auto t1 = split(move(t0.first), l);
tr = merge(merge(move(t1.first), move(t0.second)), move(t1.second));
}
}
}