概要

文字列 $S$ のSuffix Automatonとは、ざっくりいうととても性質のいいDFA(決定性オートマトン)である。一番代表的な性質は次のとおりである。

$S$ の部分文字列全て、またそれらのみを受理する。
頂点数，辺数が $O(|S|)$、より正確には $|V| \leq (2|S| - 1), |E| \leq (3|S| - 4)$
$O(|S|)$ 時間で構築可能

このようなオートマトンが存在するということがまず非自明なのだが、これらに加えて、更に様々な良い性質がある。

構築

構成

最初に、どのようなオートマトンを作るのか(および、存在性の証明)を示す。結論から言うと、Suffix Automatonは$\mathrm{rev}(S)$のCompressed Suffix Treeから機械的に作ることが出来る。

例えば、$S = "babcc"$、つまり $\mathrm{rev}(S) = "ccbab"$ の場合、Suffix Treeは次のようになる。黒色のノードは、そのノードを終端とする Suffix が存在することを表す。

f:id:yosupo:20210131160146j:plain

「次数 $1$ かつ白色のノード」を子のノードとマージしたものがCompressed Suffix Treeである。これと、$S$ の Suffix Automaton が次のようになる。

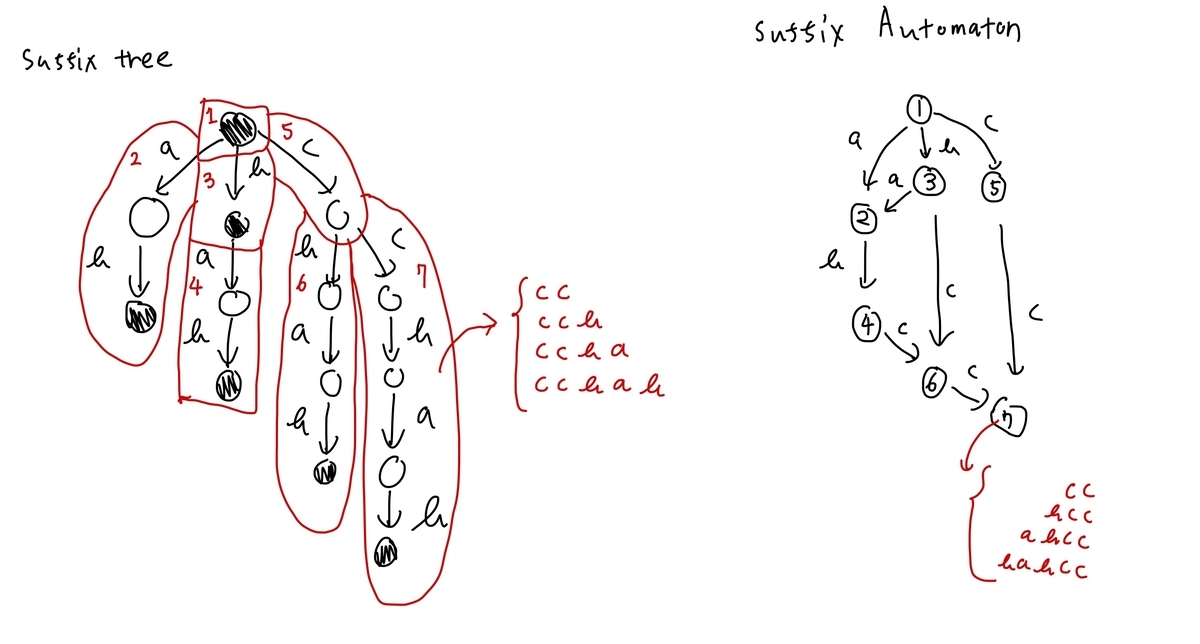
f:id:yosupo:20210131160121j:plain

ここで、左右のノードは一対一対応している。実際に、ノード7について、受理する文字列の集合が(revすると)全く同一である。他のノードに対しても同じ性質が成り立つ。

このようなAutomatonが必ず存在することが、次の定理によりわかる。証明は容易なので略する。

Compressed Suffix Treeの(根以外の)任意のノードについて、受理する文字列たちから最初の文字を削除した集合は、いくつかのノードの受理する文字列たちの直和で表せる。

実際に、Compressed Suffix Treeの各ノードについて、上記の直和のノードたちから最初の文字で遷移を貼るだけでSuffix Automatonが構築できる。

頂点数 / 辺数

頂点数は明らかに線形である(一般に、$n$ 個の文字列からパトリシアを作ると頂点数は$O(n)$になる)。

辺数はまずSuffix Automatonから(有向)全域木を取る。当然これの辺数はノード数 - 1である。全域木に含まれない辺それぞれについて、(全域木のパス + 含まれない辺)から生成される文字列たちを考える。すると

全て $S$ の部分文字列
文字列の間に、「片方が片方のprefix」という関係はない

が成立するので、文字列の個数 = 全域木に含まれない辺数は高々 $|S|$

アルゴリズム

Compressed Suffix Tree / Suffix Automaton を対応を意識しながら並列で構築する。KMPアルゴリズムのように、$S$ の後ろ($\mathrm{rev}(S)$の先頭)に一文字ずつ文字を追加していく。これは Compressed Suffix Treeでは、(新しい)文字列全体をSuffix Treeに追加することに対応する。

Compressed Suffix Tree / Suffix Automatonの情報として、次の情報を持つ。

$\text{next}(\text{node}, \text{char})$ : Suffix Automatonの辺
$\mathrm{link}(\mathrm{node})$ : Compressed Suffix Treeでの親ノード
$\mathrm{len}(\mathrm{code})$ : nodeが受理する最長の文字列の長さ(=Suffix Treeでの一番下のノードの深さ)
$\mathrm{last}$ : $S$ 全体を入れた時に受理するノード

lenだけ不自然に感じるが、構築で必要になる。

構築においての本質は、Suffix Automatonの次の性質である。

(非空の文字列) $S$ の最後の文字を削除した文字列を $S'$ とする。Compressed Suffix Treeでの $S'$ / $S$ のパス上のノードを $n'1, n'2, \cdots, n'l$ / $n_1, n_2, \cdots, n_m$ とする($n'1 = n_1 = \mathrm{根}$)。このとき、$\mathrm{根}, \mathrm{next}(n'1, x), \mathrm{next}(n'2, x), \cdots, \mathrm{next}(n'_l, x)$ をランレングス圧縮したものが、$n_1, n_2, \cdots, n_m$ となる。

構築では、新しい文字を後ろに追加した後この性質を満たすように様々な値をいじればよい。

実際には新しいノードを作り、 $\mathrm{last}$ からlinkをたどっていく。そして

$\mathrm{next}(n, x)$ が存在しない間 $\to$ 新しく作ったノードに$\mathrm{next}(n, x)$を張っていく
$\mathrm{next}(n, x)$ が存在する場合。ノード $m = \mathrm{next}(n, x)$を分割(Clone)しないといけない場合がある。この判定に $\mathrm{len}$ を使う。$\mathrm{len}(n) + 1 = \mathrm{len}(m)$ ならば Cloneする必要がない。
- 分割するためには、新規ノードを追加する。これはSuffix Treeで根から近い側に対応する。更に$m = \mathrm{next}(n, x)$ の間linkを辿り、nextを新規ノードに張り替える必要があることに注意。

構築の計算量について考える。頂点数、辺数が線形であるので大部分は大丈夫だが、唯一怪しいのは「ノードをCloneした後にnextを張り替える」部分である。実際には、「Compress Suffix Treeでの $\mathrm{last}$ ノードの高さ」をポテンシャルとすることで抑えることが出来る。

性質

その他の性質を列挙する

Suffix Automatonは「Sの部分列、またそれのみを受理する」DFAの中で頂点数が最小(らしい)
$S$ のSuffixと、cloneされてないノードたちは1対1対応する。

拡張

Compressed Suffix Treeが自然に複数の文字列に対応できるように、Suffix Automatonも対応できる。

lastを初期化して文字列追加、を同じ Suffix Automaton に繰り返せば良い。ここで、新しいノードが生まれない場合もあることに注意。

問題例

$S$ の部分文字列の種類数

DAGのパスの総数となるので、DP出来る
各頂点 $n$ について$\mathrm{len}(n) - \mathrm{len}(\mathrm{link}(n))$ を足すだけでもよい(これはCompressed Suffix Treeでのパスの長さ=受理する文字列数に対応する)。

$S, T$の共通部分列の種類数

$S$, $T$, $S$ + "$" + $T$ の部分列の個数から計算できる。
${ S, T }$ から Suffix Automaton を作ることで直接計算できる。$S$ のSuffix, $T$ のSuffixのどちらからも到達可能なノードのみについて$\mathrm{len}(n) - \mathrm{len}(\mathrm{link}(n))$を足せば良い

参考

使用例

AC code of Number of Substrings

struct SuffixAutomaton {
    struct Node {
        unordered_map<char, int> next;
        int link, len;
    };
    vector<Node> nodes;
    int last;

    SuffixAutomaton() {
        nodes.push_back({{}, -1, 0});
        last = 0;
    }

    void push(char c) {
        int new_node = int(nodes.size());
        nodes.push_back({{}, -1, nodes[last].len + 1});
        int p = last;
        while (p != -1 && nodes[p].next.find(c) == nodes[p].next.end()) {
            nodes[p].next[c] = new_node;
            p = nodes[p].link;
        }
        int q = (p == -1 ? 0 : nodes[p].next[c]);
        if (p == -1 || nodes[p].len + 1 == nodes[q].len) {
            nodes[new_node].link = q;
        } else {
            // clone node (q -> new_q)
            int new_q = int(nodes.size());
            nodes.push_back({nodes[q].next, nodes[q].link, nodes[p].len + 1});
            nodes[q].link = new_q;
            nodes[new_node].link = new_q;

            while (p != -1 && nodes[p].next[c] == q) {
                nodes[p].next[c] = new_q;
                p = nodes[p].link;
            }
        }
        last = new_node;
    }
};

int main() {
    string s;
    cin >> s;

    SuffixAutomaton sa;
    for (char c : s) {
        sa.push(c);
    }

    int m = int(sa.nodes.size());
    ll ans = 0;
    for (int i = 1; i < m; i++) {
        ans += sa.nodes[i].len - sa.nodes[sa.nodes[i].link].len;
    }

    cout << ans << endl;
    return 0;
}